The Kelly Criterion is a smart way to decide how much money to bet. It helps you bet just the right amount to grow your money steadily without the risk of losing it all. Think of it as your guide to betting wisely. It’s very popular among betters and investors for keeping risks low.
The basic Kelly Criterion formula is:
𝑓∗=(𝑏*𝑝−𝑞)/𝑏
where:
- 𝑓∗ is the fraction of the bankroll to be wagered;
- 𝑏 is the net odds received on the bet;
- 𝑝 is the probability of winning;
- 𝑞 is the probability of losing, which is 1−𝑝.
Interpretation:
- 𝑓∗: Represents the optimal fraction of your bankroll that you should bet to maximize your expected growth. If the result is 0.25, for instance, it suggests you should bet 25% of your bankroll.
- 𝑏: The multiplier associated with the bet, minus 1. For example, if you could double your money on a win ($2 back for every $1 bet, including the original bet), 𝑏 would be 1.
- 𝑝: Your assessed probability of winning the bet. This must be a value between 0 and 1, where 0.5 represents a 50% chance of winning.
- 𝑞: The probability of losing the bet, calculated as 1−𝑝.
How to Use It:
- Access your last 50 to 100 games: Most crash games have a history. Moreover, provably fair games give you full access to the game history and results. For example, third-party scripts are used to verify games on BC.Game crash game or NanoGames.
- Calculate Your Edge: Your “edge” is 𝑏*𝑝−𝑞. If this value is positive, you have an advantage over the house or the market.
- Determine Bet Size: The formula tells you the optimal proportion of your bankroll to bet to maximize growth and minimize risk.
Applying this strategy manually requires diligence in tracking and calculating. But can offer insights into the game’s patterns and your betting strategy’s effectiveness.
Example:
If you’re betting on a coin toss where you win double your bet for guessing right, and you somehow know the coin has a 51% chance of landing heads (which you bet on):
- 𝑏=1 (since you double your money on a win)
- 𝑝=0.51
- 𝑞=0.49
Plugging these into the Kelly formula gives:
𝑓∗=(1)(0.51)−0.49=0.02
This result suggests you should bet 2% of your bankroll on each toss to maximize your bankroll growth over time while minimizing risk.
Important Considerations:
- The Kelly Criterion assumes you can accurately estimate probabilities (𝑝 and 𝑞). Overestimations can increase the risk of large losses.
- It’s a long-term strategy. Short-term volatility can still result in significant drawdowns.
- Betting more than the Kelly Criterion suggests increases your risk of losing a larger portion of your bankroll. Betting less reduces the risk but also slows down bankroll growth.
Script for BC.Game’s Crash
By collecting data from 50 games, you can calculate a more accurate estimate of 𝑝 (the probability of winning) and 𝑞 (the probability of losing, which is 1−𝑝). This data enables you to refine your betting strategy based on historical outcomes, potentially improving the precision of your bets and optimizing your bankroll management.
Step 1: Collect Game Data
You would start by collecting outcomes from the last 50 games (configurable parameter). This data collection phase involves tracking whether each game reaches your target multiplier before crashing.
Step 2: Calculate Probabilities
Once you have the game data, calculate the winning probability (𝑝) by dividing the number of games that reached or exceeded your target multiplier by the total number of games observed (50 in this case).
Step 3: Apply the Kelly Criterion
With 𝑝 calculated from your data, and knowing 𝑞=1−𝑝, apply the Kelly Criterion formula to determine the optimal fraction of your bankroll to bet.
BC.Game Script Implementation
We collect game data during the game session. This approach takes some time but is more suitable if you’re confident in the game’s stability and wish to maximize the data available for analysis.
To use a Crash game script on BC.Game, follow these steps:
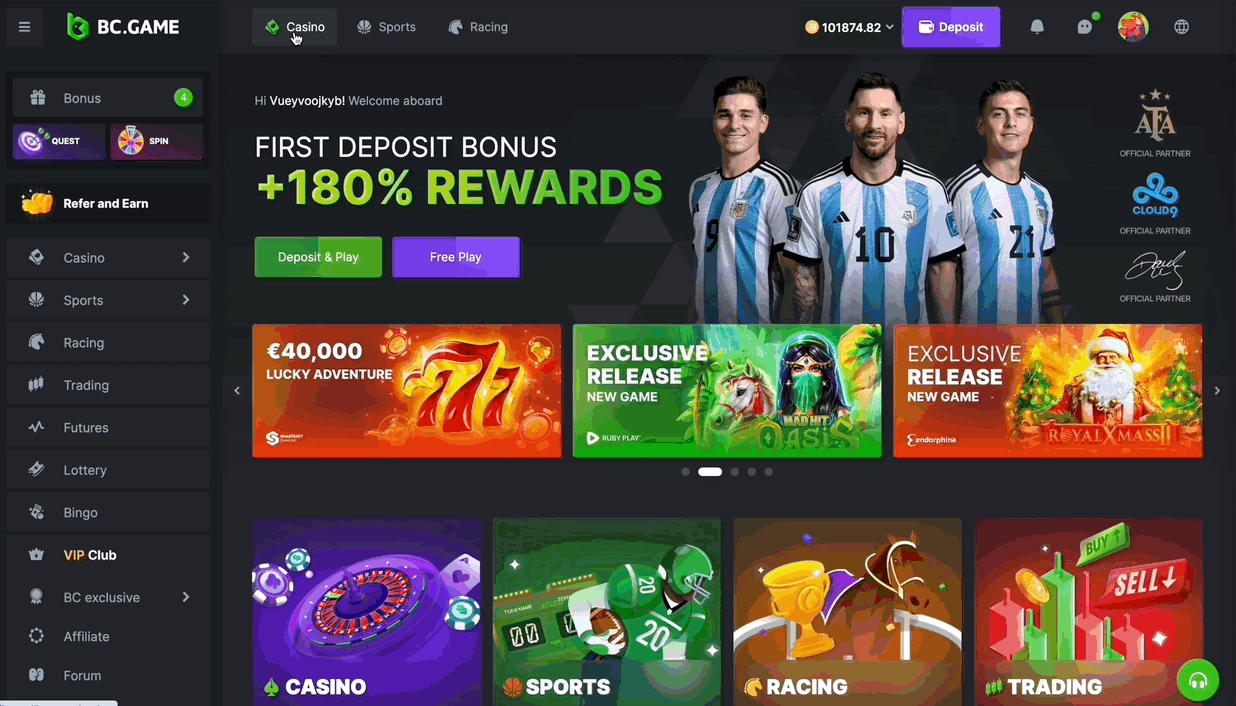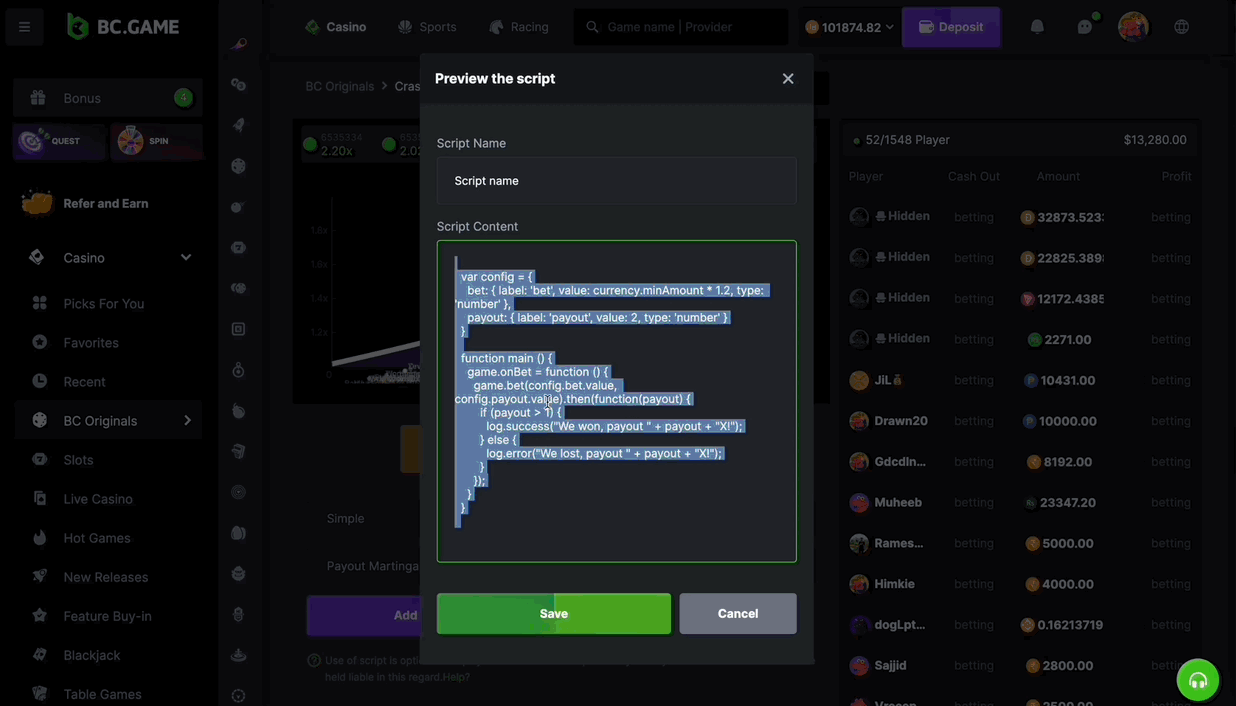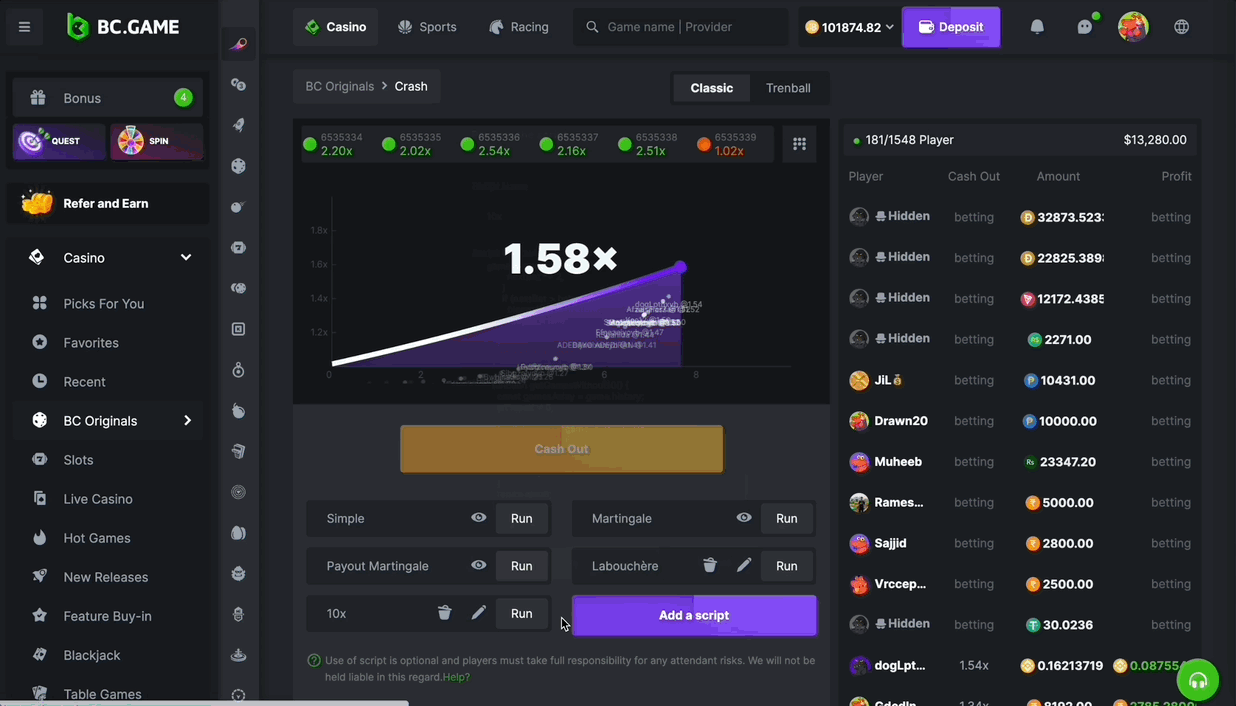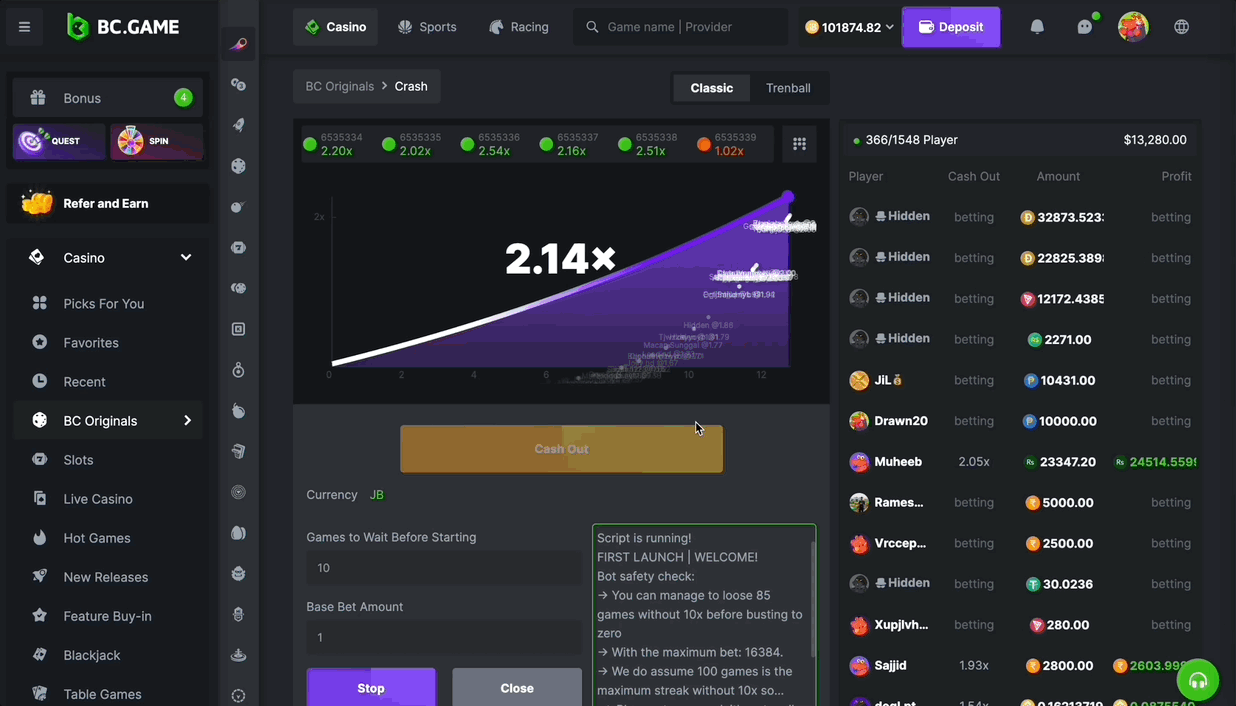
- Go to Advanced Betting Mode: In the BC Originals Crash game, switch to “Advanced” to see different crash game scripts.
- Add a Script: Press the Add Script button, put in the code for the script you want to start the automated betting, give it a name and press the Save button.
- Run Script: Turn on the script to automatically bet and possibly increase your cryptocurrency.
Important Considerations:
- Accuracy of 𝑝: The accuracy of the winning probability (𝑝) directly affects the effectiveness of the Kelly Criterion in optimizing your bet size. Ensure your data collection and analysis are as accurate as possible.
- Changing Dynamics: The crash game’s dynamics might change over time. Regularly update your data and recalibrate your strategy accordingly.
- Risk Management: The Kelly Criterion helps manage risk, but it’s based on the accuracy of your inputs (𝑝 and 𝑞). Always be cautious and consider setting aside a portion of your bankroll that is not at risk.
Summary
Summarizing the discussion on using the Kelly Criterion and analyzing game history for betting in a crash game, the strategy indeed focuses on identifying situations where the probability of winning is deemed favorable based on historical data. By calculating the win probability (𝑝) from recent game outcomes and applying the Kelly Criterion, the strategy aims to optimize bet sizes in scenarios where there’s a perceived edge—that is, where the chances of winning are higher relative to losses. Here’s how it works:
Understanding the Strategy
- Collect Historical Data: You accumulate outcomes from a certain number of recent games to analyze the game’s behavior. This dataset helps you understand the frequency of winning versus losing at your target multiplier.
- Calculate Win Probability (𝑝): By analyzing the collected data, you estimate the probability of a game reaching or exceeding your target multiplier. This win probability is crucial for determining whether you have a betting edge.
- Apply the Kelly Criterion: With the win probability (𝑝) in hand, you use the Kelly Criterion to calculate the optimal fraction of your bankroll to bet. This calculation is grounded in the logic that betting should be proportional to your edge; a higher probability of winning suggests a larger bet size, but only up to a point that balances growth with risk.
- Wait for a Positive Bet Opportunity: You wait until the calculated win probability suggests a positive expected value—that is, when the number of winning games within your dataset suggests a higher chance of winning than losing at your chosen target multiplier. Only then do you place a bet, and the size of that bet is optimized according to the Kelly Criterion to maximize long-term growth of your bankroll while minimizing risk.
The Key Advantage
The primary advantage of this strategy is that it’s data-driven and dynamic. It adapts to the current conditions of the game as reflected in the most recent outcomes. By focusing on situations where historical data indicates a higher probability of winning, you align your betting strategy with opportunities that have a statistical edge in your favor.
Important Considerations
- Data Relevance: This strategy assumes that historical game outcomes are a relevant predictor of future results, which holds true in games with consistent mechanics and probabilities.
- Sample Size and Variability: The accuracy of your win probability estimation depends on the size and variability within your dataset. Larger datasets can provide more reliable estimates but require time to collect games data and careful management to ensure relevance.
In summary, this strategy leverages the Kelly Criterion in conjunction with historical game data analysis to identify and exploit positive betting opportunities, aiming to increase the chance of winning by making informed, calculated bets.